This Little Light of Mine
- Dulcie Crowther
- Apr 10, 2020
- 4 min read
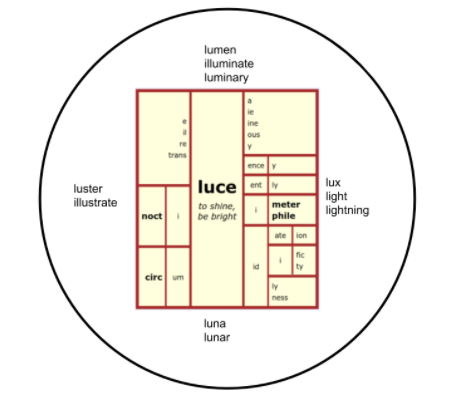
My niece gave birth to a magnificent baby girl eight weeks ago. Little Lucy May. Well, not so little. She weighed in at 10½ lbs!!! It’s the wrong time of year to say she’s a Butterball Turkey, so I’m going with a gorgeous Easter Ham. She is plump, adorable, and ripe for kissing. I did what any adoring aunt would do. I looked up her name to figure out the base element. It's <luce>, the female version of the Late Latin name Lucia which traces further back to lux meaning “light.” Next, I made her a word matrix using the base element of her name. Have you figured out yet that I’m a dork? My niece and her mom were miffed. They had no idea the jewel I had presented to them.
Allow me to explain. A word matrix is a way to elegantly organize a word family. To belong in a matrix, each word must trace back to the same single historical root word and the base element of each word must share the same structure, i.e. the same letter sequence. Words that share an historical root but do not share the same structure cannot be in the matrix, but they can be in the family circle. Here are the rules on how to use this matrix.
Rule #1: Read word matrices from left to right.
Rule #2: All words built from a word matrix must include the base element which has a box all to itself and is in bold lettering. It holds the denotation (the literal meaning of the base). The base element is either a free base (can stand alone as a word) or a bound base (needs affixes to make it a word).
Rule #3: Just because you CAN make a word doesn’t mean it IS a word. *noctilucidation is not a word as far as I know.
Rule #4: You do not have to start with the first box, and neither do you have to use all the boxes.
Rule #5: Wherever you decide to start making a word, from that point on, you cannot skip over a box. If I start with the base <luce>, I can’t skip to <ly> and make the word <lucely>, but I could make <luce/ + ent + ly → lucently>
Rule #6: This rule is called a spelling convention - when a base element has a final, nonsyllabic <e> (i.e. a silent <e> at the end of a base), and you are adding a vowel suffix (a suffix that begins with a vowel), replace the <e> with the vowel suffix. If I were writing a word sum by hand, I would simply cross out the <e>. On a computer, I would note the dropping of that <e> with a slash after it like this - <trans + luce/ + ence → translucence>
Here’s the fun part. On the count of three, you have 60 seconds to make as many words as you can. Pencils up! Backs straight! Feet flat on the floor! Go! (See bottom for answers)
Sorry. This one might be a bit challenging on the first go-round. Admittedly, I don’t know most of these words either! I just chose ones that seemed fun and positive keeping our twinkling little star Lucy in mind. Because what’s not fun about noctilucent organisms like plankton that glow in the dark?! While I consulted Merriam and Webster and Doug Harper on a few words, I mostly consulted Mr. John Rayona at Word Information to find the majority of the words used. Even though I’m not familiar with the words, I am familiar with the sense and meaning of the base and affixes. I don’t exactly know what <elucid> means, but knowing there is a prefix <e> that means “away from” and knowing that <luc(e)> means “light,” I could make a pretty good guess on an SAT exam at that word’s meaning given a sentence. Buy one base element, get many words for free.
How much more compact would vocabulary and spelling instruction be if we didn’t learn words one at a time, if we didn’t have to “just sound it out,” but were taught from the start that words belong to a family? And family members share meaning and tend to look alike. If you asked me to spell <elucid> and told me it meant “to give off light” (because you know how I love a good on-the-spot spelling test), I probably wouldn’t “just sound it out” and spell it *eeloosud. I would consider its meaning and its family members while I considered what sounds I heard in the word. My hope for you, Little <Luce/+ y -->Lucy> May, is that when you reach pre-K and Kindergarten, you’ll learn to read, spell, and make meaning of words based on their family first, and how they sound second.
Do you want to know the real kicker about Lucy May, our scrumptious Easter Ham? This cutest ever Butterball Turkey? Her last name is Noel. Yeah, she’s definitely going to be the brightest Christmas light in our family this year and for many more to come.
Answers: circumlucid, elucid, elucidate, elucidation, illucidate, illucidation, lucent, lucimeter, luciphile, noctilucence, noctilucent, noctilucous, relucence, relucent, translucent, translucence, translucency, translucent, translucently. Feel free to make words that are not in a dictionary. If you can use it correctly in a sentence, it’s a word.



Comments